자료구조 정리

자료구조 정리

Stack

FILO (First-in-last-out) 자료구조

• 마지막에 들어간 데이터가 가장 처음 나온다

Queue

FIFO (First-in-first-out) 자료구조

• 처음에 들어간 데이터가 가장 처음 나온다

Circular Queue

Front와 Rear를 가진 Queue

• POP하면 Front가 +1 이 되고 PUSH를 하면 Rear가 +1 이 됨
• Rear는 마지막 데이터 바로 뒤에 위치하고, 만약 Rear == Front 라면 꽉찬 것

Linked List

데이터의 앞 뒤가 서로 링크로 연결된 자료 구조

• 다음, 이전 데이터 접근 쉬움
• 임의의 데이터를 찾는데 O(N) 시간 걸림
• 데이터 삭제, 삽입이 빠름
  • 삭제, 삽입 시 해당 위치 좌우의 데이터의 링크만 잘 조정해주면됨

Tree

Binary Tree

루트 노드와, 그 루트 노드의 좌측, 우측 자식 노드로 구성된 트리

• Full Binary Tree : Binary Tree가 균형적이게 꽉찬 트리
• Complete Binary Tree : Full은 아니지만, Depth - 1까지는 Full이고, Depth는 좌측부터 시작해서 차례대로 차 있는 트리

• 배열이나, Link로 구현 가능

• Preorder Traversal (전위 순회)
  • 노드를 들리고 좌측 자식 -> 우측 자식 순으로 탐색

void preorder(treePointer ptr) {
  if(ptr) {
    printf("%d", ptr->data);
    preorder(ptr->leftChild);
    preorder(ptr->rightChild);
  }
}

• Inorder Traversal (중위 순회)
  • 좌측 자식이 없을 때까지 간 다음 들리고, 그 후 우측 자식 봄

void inorder(treePointer ptr) {
  if(ptr) {
    inorder(ptr->leftChild);
    printf("%d", ptr->data);
    inorder(ptr->rightChild);
  }
}

• Postorder Traversal (후위 순회)
  • 좌측 Subtree 그 다음 우측 Subtree 후 Root 방문

void postOrder(treePointer ptr) {
  if(ptr) {
    postOrder(ptr->leftChild);
    postOrder(ptr->rightChild);
    printf("%d", ptr->data);
  }
}

• Levelorder Traversal (레벨 순회)
  • Depth 순서대로 방문한다

Queue Q;
Q.push(1);
while(!Q.empty()) {
  visit(Q.front());
  Q.pop();
  Q.push(leftChild);
  Q.push(rightChild);
}

Priority Queue (Max or Min Heap)

우선 순위가 높은 것 (값이 제일 크거나, 작거나 등) 부터 먼저 꺼내는 큐

void siftDown(vector<int>& arr, int idx) {
	int m = -1;
	if (arr.size() > idx * 2 + 1)
		m = arr[idx * 2] < arr[idx * 2 + 1] ? idx * 2 : idx * 2 + 1;
	else if (arr.size() > idx * 2)
		m = idx * 2;
	if (m != -1 && arr[idx] > arr[m]) {
		swap(arr[idx], arr[m]);
		siftDown(arr, m);
	}
}

void makeHeap(vector<int>& arr) {
	for (int i = arr.size() / 2; i >= 0; i--)
		siftDown(arr, i);
}

int pop(vector<int>& arr) {
	int top = arr[0];
	arr[0] = *(arr.end() - 1);
	arr.resize(arr.size() - 1);
	siftDown(arr, 0);
	return top;
}

vector<int> arr = { 2, 4, 5, 3, 1, 9, 6, 7, 10, 8 };
makeHeap(arr);
while (arr.size() > 0)
	printf("%d\n", pop(arr));

Binary Search Tree

루트에서 작은 데이터는 좌측 큰 데이터는 우측으로 나눠서 데이터 관리

• 빠른 검색 가능
• 탐색의 경우 O(H)의 시간이 걸림 (H는 높이)
• 입력, 삭제 연산의 경우 O(1)이 걸림
• 이진 검색 트리에 inorder 순회 (주위 순회)를 할 경우 값이 정렬되게
• 삽입 연산
  1. 위치 검색
  2. 삽입
• 삭제 연산
  1. 자식 노드가 없는 경우
     • 그냥 삭제하면됨
  2. 자식 노드가 하나 있는 경우
     • 해당 노드를 지우고 해당 노드의 자식과 부모를 연결
  3. 자식 노드가 두 개 있는 경우
     • inorder 순회를 통해서 삭제 하려는 노드의 Successor(바로 뒤) 노드를 탐색하고 해당 노드를 삭제할 위치로 옮기면됨, 그리고 해당 노드가 옮겨지면서 발생하는 빈자리 또한 1. 2. 의 규칙에 따라 정렬해 나가면됨 (왜냐하면 Successor의 경우 삭제 하려는 노드의 우측 서브 트리에서 가장 작은 값이므로 자식을 최대 하나만 가진다고 보면됨)

Forest

트리를 여러개 가지는 자료구조

Disjoint Set

Union으로 두 집합을 묶을 수 있고, Find로 집합의 최상위 부모가 누구인지 찾는 자료 구조

• 집합의 결합이 매우 쉬움

int parent[100];

void Union(int a, int b) {
	parent[find(b)] = find(a);
}

int find(int idx) {
	if (parent[idx] == idx) return idx;
	return (parent[idx] = find(parent[idx]));
}

int main() {
	for (int i = 0; i < 100; i++)
		parent[i] = i;

	return 0;
}

Graph

Vertex와 Vertex와 Vertex를 잇는 Edge로 구성된 자료 구조

• Directed Graph : Edge가 방향성을 가지는 자료 구조
• Complete Graph : 모든 Vertex가 연결되어 있을 경우
• Sub Graph : 어떤 Graph의 부분 집합
• in-degree : Vertex에 들어오는 Edge 수
• out-degree : Vertex에서 나가는 Edge 수
• Cyclic : 싸이클을 가지는 Graph

• Adjacency Matrix로 표현 가능

  	1	2	3	4
  1	0	1	1	1
  2	1	0	1	1
  3	1	1	0	1
  4	1	1	1	0

• Adjacency List로도 표현 가능

Depth First Search

Stack을 이용해서 구현 가능

• 현재 Vertex에서 갈 수 있는 Vertex 중 하나를 Stack에 넣고 현재 Vertex 방문 표시
• Stack에서 Vertex를 꺼내서 위의 과정 반복 (방문 하지 않은 곳만 Stack에 넣음)
• 갈 수 있는 곳이 없으면 POP

Breadth First Search

Queue를 이용해서 구현 가능

• 현재 Vertex에서 갈 수 있는 Vertex들 모두를 Queue에 넣음
• Queue에서 Vertex를 꺼내서 다시 갈 수 있는 Vertex들을 방문 하는 것을 반복

Hashing

Dictionary 쌍을 O(1) 시간에 찾을 수 있도록 해주는 자료구조

Static Hashing

• Hash table : Dictionary 들이 저장되어 있는 테이블
• Buckets b : Hash table은 N개의 Bucket으로 나뉘어져 있고, 하나의 Bucket은 s개의 Dictionary 쌍 들을 가질 수 있음
• Slots s : Bucket에서 s개의 Dictionary 쌍을 가질 수 있다는 것을 slot이 s개 있다고 표현함, 보통 Slot = 1
• Hash function H : Dictionary의 Key K와 Bucket B를 맵핑해주는 함수
  • H(K) = 0 ~ (b - 1) 까지 할당해주는 함수
• Hash : K의 Hash는 H(K) 임, Home address라고도 부름
• Key Density : (Dictionary 갯수 N) / (Key가 될 수 있는 모든 경우의 수 T)
• Loading Density : n / sb
• 보통 Key Density가 아주 작기 때문에 Hash Function이 하나의 Bucket안에 몇몇개의 Key가 있도록 한다 (Hash Table이 너무 커지지 않도록 하기 위해)
• Synonyms : H(k1) == H(k2) 일 경우 k1과 k2를 synonym이라 함
• Overflow : Bucket에 Slot이 남아 있지 않은데 데이터 넣으려 할 경우
• Collision : Bucket이 비어있지 않을 때 데이터 넣는 경우
• Insert, delete, find 는
  • Overflow가 일어나지 않을 경우 O(s)
  • Collision이 일어나지 않을 경우 O(1)

Hash Functions

계산하기 쉽고, Collision의 수를 최소화하는 함수가 좋음

• Uniform Hash Function : H(k) = i 일 확률이 모든 Bucket i에 대해서 1/b일 경우
• 보통 Key를 정수로 변환한 다음 사칙 연산을 써서 함수를 만듬

Division

Hash Function H(k) = k % D

• 가장 쉽고 자주 쓰임

Mid-Square

Hash Function H(k) = select_mid(k * k)

• Key 값을 제곱한 다음 중간 몇 자리를 사용

Folding

• Shift Folding : 값을 일정 크기로 나눈 후 모두 더함
  • eg) 1234567890 => 123 + 456 + 789 + 0 = 1368
• Folding at the boundaries : 짝수 번째 파티션을 역으로 치환한 다음 더함
  • eg) 1234567890 => 123 + rev(456) + 789 + rev(0) = 123 + 654 + 789 + 0 = 1566

Digit Analysis

키 값을 모두 알 경우, 키 값을 구성하는 digit들의 분포를 이용함

• 키 값 중 분포가 일정한 숫자들을 뽑음

  • eg) 1, 3, 5 번째 숫자를 쓴다면

    Key	H(Key)
    134123	142
    534125	542
    23425	245

String Key를 양의 정수로 변환

unsigned int stringToInt(char *key) {
	unsigned int sum = 0;
	while (*key)
		sum += *key++;
	return sum;
}

Overflow Handling

Hashing 시 Overflow 방지 방법

Open Addressing

이미 Hashtable에 H(k)가 있을 경우 다음 Bucket에 결과 삽입

• 아래의 경우 function이 if와 Hash가 같기 때문에 if의 다음 Bucket인 0에 삽입

  Key	H(Key)
  for	2
  do	3
  while	4
  if	12
  else	9
  function	12

  index	value
  0	function
  1
  2	for
  3	do
  4	while
  5
  6
  7
  8
  9	else
  10
  11
  12	if

• Linear Probing 으로 테이블 검색

  1. H(K) 계산
  2. HT[H(K)], HT[(H(K) + 1) % b], … , HT[(H(K) + j) % b]를 찾음
     1. HT[(H(K) + j) % b]가 K라면 찾음
     2. HT[(H(K) + j) % b]가 비었다면 못 찾음
     3. 다시 시작지점인 HT[H(K)]로 돌아온다면 못 찾은 것

Chaining

Collision이 일어났을 경우 해당 Bucket의 가장 뒤에 새로운 Key를 삽입

• Key끼리 링크로 이어짐

Efficient Binary Search Trees

Optimal Binary Search Tree - 트리의 Depth가 log_2(N)인 트리

AVL Tree

Vertex T에서 Balance Factor BF(T)가 1, 0, -1 중 하나인 Tree

• Balance Factor는 H_L - H_R (좌측 서브트리의 높이, 우측 서브트리의 높이)
• Binary Search Tree 이면서 Balanced되게 해줌
• 노드 삽입 시 Balance Factor를 검사해서 2이상이거나 -2이하이면 자신의 자식을 검사하여 좌 혹은 우로 회전시켜야할지 결정한다
  • Balance Factor가 2 이상일 경우
    • 현재 삽입하려는 값이 현재 노드의 좌측 자식 노드 값 보다 작을 경우
      • Left Left의 경우로 현재 노드를 우측으로 회전시킨다
    • 현재 삽입하려는 값이 현재 노드의 좌측 자식 노드 값 보다 클 경우
      • Left Right의 경우로 좌측 자식 노드를 좌측으로 회전시킨 다음 현재 노드를 우측으로 회전시킨다
  • Balance Factor가 -2 이하일 경우
    • 현재 삽입하려는 값이 현재 노드의 우측 자식 노드 값 보다 클 경우
      • Right Right의 경우로 현재 노드를 좌측으로 회전시킨다
    • 현재 삽입하려는 값이 현재 노드의 우측 자식 노드 값 보다 작을 경우
      • Right Left의 경우로 우측 자식 노드를 우측으로 회전시킨 다음 현재 노드를 좌측으로 회전시킨다
• 노드 삭제 시 Binary Search Tree와 동일하게 삭제 후 위와 같이 밸런스를 맞추어 주면 됨

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>

using namespace std;

typedef struct vertex {
	string key;
	int height = 1;
	struct vertex* left = NULL;
	struct vertex* right = NULL;
} vertex;

vertex* makeNode(string key) {
	vertex* node = new vertex;
	node->key = key;
	return node;
}

int height(vertex *ver) {
	return ver == NULL ? 0 : ver->height;
}

vertex* rotateRight(vertex* ver) {
	vertex* left = ver->left;
	vertex* right = left->right;
	left->right = ver;
	ver->left = right;

	ver->height = 1 + max(height(ver->left), height(ver->right));
	left->height = 1 + max(height(left->left), height(left->right));
	return left;
}

vertex* rotateLeft(vertex* ver) {
	vertex* right = ver->right;
	vertex* left = right->left;
	right->left = ver;
	ver->right = left;

	ver->height = 1 + max(height(ver->left), height(ver->right));
	right->height = 1 + max(height(right->left), height(right->right));
	return right;
}

vertex* insertVertex(vertex *ver, string key) {
	if (!ver) return makeNode(key);

	if (ver->key > key)
		ver->left = insertVertex(ver->left, key);
	else if (ver->key <= key)
		ver->right = insertVertex(ver->right, key);

	ver->height = 1 + max(height(ver->left), height(ver->right));

	int balance = height(ver->left) - height(ver->right);
	// Left Left
	if (balance >= 2 && ver->left->key > key)
		return rotateRight(ver);

	// Right Right
	if (balance <= -2 && ver->right->key < key)
		return rotateLeft(ver);

	// Left Right
	if (balance >= 2 && ver->left->key < key) {
		ver->left = rotateLeft(ver->left);
		return rotateRight(ver);
	}

	// Right Left
	if (balance <= -2 && ver->right->key > key) {
		ver->right = rotateRight(ver->right);
		return rotateLeft(ver);
	}

	return ver;
}

void inorder(vertex* ver) {
	if (ver) {
		inorder(ver->left);
		cout << ver->key << " ";
		inorder(ver->right);
	}
}

int main() {
	vector<string> month = {
		"MAR", "MAY", "NOV", "AUG", "APR", "JAN",
		"DEC", "JULY", "FEB", "JUNE", "OCT", "SEPT"
	};
	// AVL Tree
	vertex* root = NULL;

	for (string m : month)
		root = insertVertex(root, m);
	inorder(root);
	return 0;
}

Red-Black Tree

Balanced Binary Search Tree를 만들기 위한 또 다른 방법

• 아래 규칙을 지켜야한다.
  1. 루트와 모든 리프(NULL)는 검정색 이어야 한다.
  2. 루트에서 모든 리프까지 경로에는 연속되는 붉은색 노드가 없어야한다.
  3. 루트에서 모든 리프까지 가는 경로의 검정색 노드 갯수는 동일해야한다.
• 레드블랙 트리의 경우 특이하게 리프노드가 NULL인 걸 명심
• 레드블랙 트리에서 삽입
  1. 삽입된 노드(N)는 무조건 붉은색으로 들어감
  2. N의 삼촌(부모의 형제)이 붉은색이라면, 부모와 삼촌 노드를 검정색으로 바꾸고 조상 노드를 붉은색으로 바꿈
     • 조상 노드의 부모가 붉은색이라면 재귀적으로 색을 바꿔서 올라감
     • 루트까지 가면 검정색으로 바꾼 후 끝내면됨
  3. N의 삼촌이 검정색이라면
     • N이 부모의 우측 자식이면 AVL Tree에서 처럼 좌측으로 회전
     • 위의 방법 후 혹은 N이 부모의 좌측 자식이면 N의 부모를 검정색으로 조부모를 붉은색으로 바꾼 후 우측 회전
• 노드 삭제 시 Binary Search Tree와 동일하게 삭제 후 위와 같이 밸런스를 맞추어 주면 됨
  • Successor를 삭제하려는 노드 N 자리에 가져다 놓고 (값 복사) Successor를 삭제
    • 색상은 바뀌지 않으므로 괜찮음
  • Successor의 빈자리를 매꾸는 과정에서 다시 정렬 필요함
    • 하지만 Successor는 자식을 하나만 갖거나 갖지 않기 때문에 해당 경우에 국한해 설명 가능
    • Successor가 붉은색이고 자식이 검정색이라면 그냥 지우면 된다.
    • Successor가 검정색이고 자식이 붉은색이라면 자식의 색을 겁정색으로 바꾸고 Successor를 지우면 된다.

    

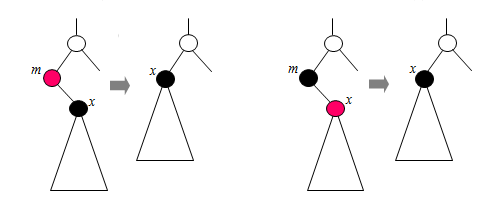
    • 하지만 만약 Successor와 자식이 모두 검정색일 경우 레드블랙 트리의 3. 규칙인 루트에서 모든 리프까지 가는 경로의 검정색 노드 갯수가 동일해야한다는 규칙이 깨지기 때문에 균형을 맞춰줘야한다.
    • kkd927님 블로그 참고

Multiway Search Tree

이진 검색 트리 처럼 두 개의 자식만 가지는게 아닌 트리의 Degree(Order) 만큼 자식을 가지는 트리

B Tree

D = Degree, T = ceil(M/2)

• 특징
  1. 루트 노드가 리프인 경우를 제외하고는 항상 최소 2개의 자식을 가짐
  2. 루트 노드와 리프 노드를 제외한 모든 노드들은 최소 T, 최대 D개의 서브 트리를 가짐
  3. 모든 리프 노드들은 같은 레벨에 존재
  4. 새로운 키가 들어오면 리프 노드에 삽입됨
  5. 노드 내 키 값들은 오름차순으로 정렬됨
  6. 리프 노드는 최소 T - 1개의 키를 가지고 있어야 함
• 삽입
  1. 키를 노드에 삽입할 때 오름차순으로 항상 정렬해야함
  2. 노드에는 D-1개의 키를 가질 수 있고, 노드에 D번째 키를 삽입하는 순간 Overflow 발생
  3. Overflow 발생 시 노드의 중간값을 부모로 올림 (D가 짝수일 경우 D/2 - 1 번째)
• 삭제
  1. Internal 노드 삭제 시
     1. 해당 노드의 키 K가 삭제된다면, 해당 노드 좌측, 우측 자식 노드의 키 갯수가 T개 이상인지 확인 후 좌측 노드에서 빌려온다면 가장 큰 값을 우측 노드에서 빌려온다면 가장 작은 값을 올린다
     2. 만약 좌, 우 자식들의 키 갯수가 모두 T 미만 이라면 자식들을 Merge 한다 (합친다)
  2. Leaf 노드 삭제 시
     1. 리프 노드 R의 원소가 T개 이상일 경우 R에서 키를 삭제
        • 만약 키 삭제 후 R의 부모(P)와 부모의 형제(S)중 하나가 모두 T 미만이라면 P와 S, 그리고 P의 부모를 Merge 한다
     2. R의 원소 개수가 T 미만 일 경우 R에서 키 삭제 후 부모에서 키를 하나 가져오고, R의 형제로 부터 부모로 키를 하나 올린다
        • R과 R의 형제가 모두 T개 미만의 키를 가질 경우 Merge 한다
        • 부모의 키 개수가 T 미만이면 2.1. 에 따라 재귀적으로 해결한다

B+ Tree

Index 노드와 Data 노드로 나뉘어짐

• Data 노드 : 리프 노드들
  • Data 노드는 링크드리스트로 서로 연결되어 있다
• Index 노드 : 리프를 제외한 노드들
• 삽입
  1. Overflow시 D(Degree)가 홀수인 경우 T - 1번째 키를 상위로 올린다
  2. Overflow시 D가 짝수인 경우 T 번째 키를 상위 Index 노드로 올린다
  3. 2.에서 Index 노드가 Overflow라면 재귀적으로 올린다
• 삭제
  1. B+ 트리에서는 리프 노드에서 삭제가 진행됨
  2. 삭제된 키값이 Index 노드에 있어도 그대로 보존함
  3. 노드의 키 갯수가 T 미만이고 노드의 형제 키 갯수가 T 이상일 경우 키를 가져온다
     • 이 때 Merge 가능하면 합치고 Index 노드의 키를 삭제한다
  4. 3.의 Merge를 통해서 Index 노드의 자식이 T 미만일 경우 형제 Index 노드로 부터 Data 노드를 가져온 후 Index 노드를 정렬한다